Basic Training in condensed matter physics

Equation of Motion Approach to Many Body Physics
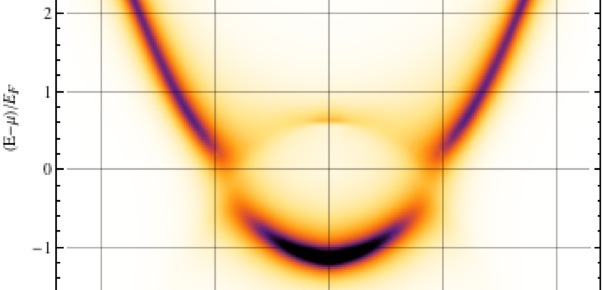
More is Different. The collective behavior of a system of interacting particles is much more rich than the behavior of a single atom. This module presents techniques for analyzing the properties of a quantum many-body system.
The Module is structured so as to be useful for both beginners who have no previous experience with quantum field theory, as well as more advanced students. It is self-contained, and all of the basic machinery will be developed. The main technique introduced, Equations of Motion, is extremely powerful, yet is not a standard part of most many-body physics courses. The resulting structure will be a form of quantum Boltzmann equation which will allow us to address non-equilibrium problems.
I personally feel that the hard part about many-body physics is not performing the calculations [you can write a computer program to calculate Ferynman diagrams for you]. The hard part is understanding why one does various things, and how to connect all of the various tools which are introduced. A good analogy is with Calculus: most of the time doing integrals is straightforward, but when you first encounter the integral sign it is mysterious and scary. I will attempt to do more than just a formal development of the theory, but will try to focus on the physical significance of the various mathematical objects. Having said this, it will be a course on technique, and there will not be any one overarching physical system which we are trying to understand.
While there will be an emphasis on the physical significance of the various concepts, this will largely be a module about techniques.
There will be 7 homework assignments. Short assignments will be given on Wednesdays, due in 2 days. Longer assignments will be given on Fridays, due in 5 days.
All are welcome, including first year graduate students in physics or other departments.
In-class participation will be expected.
Instructor:
Erich Mueller
Clark 514A
em256@cornell.edu
Dates/Times:
Jan 25 - Feb 19
Rockefeller 230
Wed. and Fri. 2:30-4pm
TextS:
(copies of relevant sections will be provided)
Kadanoff and Baym, Quantum Statistical Mechanics
Wen, Quantum Field Theory of Many-Body Systems
Prerequisites:
Quantum Mechanics [Heisenberg Representation, Second Quantization]
Statistical Mechanics [Partition Functions, Thermodynamics, some exposure to Kinetic Theory]
About the Module
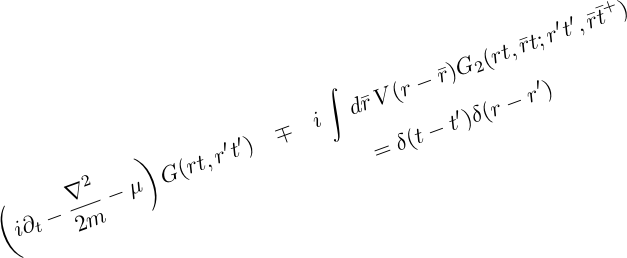
Outline
Wednesday January 27, 2009 -- Mathematical Introductions
Reading: Kadanoff and Baym, chapter 1 (and some of chapter 2)
This lecture will introduce much of the formal structure we will need for the rest of the module. These include various Greens functions, time ordering, spectral densities, and imaginary time.
Homework: p683hw1.2010.pdf -- due Friday January 29, 2010 -- p683sol1.2010.pdf
Friday January 29, 2009 -- Information contained in the Greens functions
Reading: Kadanoff and Baym, chapter 2
This lecture will explore how to extract thermodynamic functions from the greens functions, and analyze their analytic structure.
Homework: p683hw2.2010.pdf -- due Wednesday February 3, 2010 -- p683sol2.2010.pdf
Wednesday February 3, 2010 -- Path Integrals
Reading: more thorough discussion is in Wen, chapter 1-3
This lecture will give a very brief overview of the more common approach to quantum field theory, namely the path integral approach. It will be more a tour of what would be done in a course on path integrals than a full exposition. For example, we will state that Coherent States, Grassman Variables, and Wicks theorem all exist, but we will not derive any of this structure from first principles. Feynman diagrams will be introduced, but we will not address how to systematically calculate them. The main purpose of this lecture is to show how the Equation of Motion approach relates to the Path Integral approach.
Homework: p683hw3.2010.pdf -- due Friday February 5, 2010
Friday February 5, 2010 -- Equations of Motion
Reading: Kadanoff and Baym, chapter 3-4
Here we use Hamilton’s equations for the field operators to derive sets of coupled partial differential equations satisfied by the Greens functions. We learn how to make approximations to these equations, and calculate the Greens functions.
Homework: p683hw4.2010.pdf-- due Wednesday February 10, 2010
Wednesday February 10, 2010 -- Kinetics and Hydrodynamics
Reading: Landau and Lifshitz, Physical Kinetics
In this lecture we step back and review classical kinetic theory, and its connection to hydrodynamics. This will allow us in future lectures to understand the structures in our equations of motion
Homework: None
Friday February 12, 2010 -- Deriving Boltmann equations from Greens Functions
Reading: Kadanoff and Baym, chapter 6-7, 9
This lecture is in many ways the punch line of the course. We will derive a Boltzmann equations from the equations of motion for the Greens function. This gives a nice physical picture of the self-energy, and is a powerful calculational tool. This material is scattered throughout 3 different chapters of Kadanoff and Baym [do not worry that we are going to cover everything from those 3 chapters in 1 lecture].
Homework: p683hw5.2010.pdf -- due Wednesday February 17, 2010
Wednesday February 17, 2010 -- Collective Modes
Reading: Kadanoff and Baym, chapter 7,10
Here we linearize the quantum Boltzmann equation, deriving some classic results such as the Random Phase Approximation
Homework: p683hw6.2010.pdf -- due Friday February 19, 2010
Friday February 19, 2010 -- Nontrivial Examples
Reading: TBA
Having so far talked only about rather simple systems, we will spend our last lecture discussing some examples of different many-body systems, the structure of their Greens functions, and how they can be studied through the equation of motion technique.
Homework: no homework